Regresyon analizi, bir bağımlı değişkenin bir veya daha fazla bağımsız değişken tarafından açıklanmaya çalışıldığı bir ilişki inceleme yöntemidir. Bu analizin detayları ve temel kavramları daha önce ilgili bölümlerde verilmiştir. Şimdi ise SPSS ortamında tek değişkenli ve çok değişkenli regresyon analizinin nasıl yapılacağı, analiz sonuçlarının nasıl değerlendirileceği ve yorumlanacağı üzerinde durulacaktır. Bir örnek uygulama yaparak, regresyon analizi sonuçlarını değerlendirmeye ve yorumlamaya çalışacağız.
Kaynak: Altunişik, R., Coşkun, R., Bayraktaroğlu, S., & Yildirim, E. (2007). Sosyal bilimlerde araştırma yöntemleri. Sakarya Yayıncılık, Sakarya, 226, 103-118.
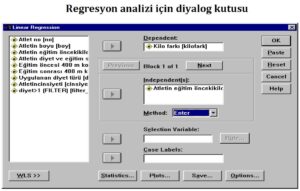
SPSS programında regresyon analizi yapmak için Analyze (Analiz) menüsünden başlayarak, sırasıyla Regresyon (Regression) ve Linear (Doğrusal) seçeneklerini seçerek doğrusal regresyon diyalog kutusuna ulaşabilirsiniz. Bu diyalog kutusunda, bağımlı değişken olarak düşündüğünüz değişkeni sol tarafta bulunan listeden seçerek, aktarma butonuyla sağ tarafta yer alan “Dependent” yazan kısma aktarmanız gerekmektedir. Ardından, ekranın sol tarafındaki listeden bağımsız değişken(ler)i seçerek, bunları “Independent(s)” yazan kısma taşımanız gerekmektedir.
Sonraki adımda, SPSS’te regresyon yöntemini seçmeniz gerekmektedir. SPSS’te beş farklı yöntem bulunmaktadır. Enter yönteminde, tüm bağımsız değişkenler aynı anda analize dahil edilir. Stepwise yönteminde ise bağımsız değişkenler, en açıklayıcı olanından daha az açıklayıcı olana doğru adım adım analize dahil edilir; bu süreç, yeni bir değişkenin katkısı olmadığı duruma kadar devam eder. Remove yaklaşımında ise önce tüm değişkenler birlikte analize dahil edilir, ardından tek tek katkı sağlamayan değişkenler modelden çıkarılır. Gerekli seçimleri yaptıktan sonra, OK butonuna tıklayarak analizi başlatabilirsiniz.
Kaynak: Altunişik, R., Coşkun, R., Bayraktaroğlu, S., & Yildirim, E. (2007). Sosyal bilimlerde araştırma yöntemleri. Sakarya Yayıncılık, Sakarya, 226, 103-118.
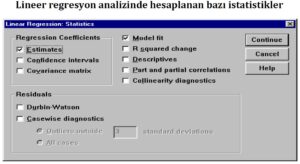
Regresyon analizi sırasında isteğe bağlı olarak çeşitli istatistikler hesaplanabilir. Bu istatistikler, regresyon modelinin performansını değerlendirmek için yapılan hesaplamaları içerir. Yukarıda (Linear Regression: Statistics) görülen istatistikler arasında regresyon katsayılarına ilişkin olanlar (katsayı tahmini, güven aralığı ve kovaryans matrisi), modelin uygunluğuna dair istatistikler (model uyumu), tanımlayıcı istatistikler (descriptives), kısmi ve kısım korelasyonlar, kolinearite analizi (çoklu doğrusallık), otokorelasyon ve hata terimlerine ilişkin analizler yer alır. Bu istatistikler, regresyon analizi sonuçlarını daha ayrıntılı bir şekilde değerlendirmek ve modelin gücü hakkında daha fazla bilgi sağlamak amacıyla kullanılır.
Kaynak: Altunişik, R., Coşkun, R., Bayraktaroğlu, S., & Yildirim, E. (2007). Sosyal bilimlerde araştırma yöntemleri. Sakarya Yayıncılık, Sakarya, 226, 103-118.
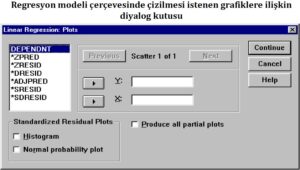
SPSS ortamında regresyon analizi sonucunda oluşturulan modelle gözlemlenen veriler ve hata terimleri arasında çeşitli grafikler elde etmek mümkündür. Bu grafikler, regresyon analizinde karşılaşılan sorunların tespiti veya çözümü için kullanılır. Bu grafikler, regresyon analizinin doğruluğunu ve modelin uygulanabilirliğini değerlendirmeye yardımcı olabilir. Örneğin, gözlemlenen verilerin bağımlı değişkene karşı dağılımını gösteren dağılım grafiği çizilebilir. Bu grafik, verilerin regresyon modeliyle uyumlu olup olmadığını görmek için kullanılır. Diğer bir grafik ise regresyon hatasının bağımsız değişkene karşı dağılımını gösteren hatayı dağılım grafiğidir. Bu grafik, modelin doğruluğunu değerlendirmek ve hata terimlerinin dağılımını incelemek için kullanılır. Ayrıca, regresyon analizinde çoklu doğrusallık sorunuyla karşılaşılıyorsa, bağımsız değişkenler arasındaki ilişkiyi gösteren çizgi grafiği veya scatterplot grafiği çizilebilir. Bu grafikler, regresyon analizindeki sorunları belirlemek ve çözmek için kullanılan önemli araçlardır.
Regresyon analizi sırasında (Linear Regression: Save) sekmesinde, çeşitli amaçlarla kullanılan değerler yer almaktadır. Bu değerler, analiz sonuçlarını kaydetmek ve ileride başka analizlerde kullanmak için kullanılabilir. Bu değerlerin sayısı ve kullanım amacı, yapılacak analizlere ve araştırma amaçlarına bağlı olarak değişebilir. Örneğin, analiz sonucunda hesaplanan tahmin değerleri veya standart hatalar, gelecekteki tahminler veya modelin doğruluğunun değerlendirilmesi için kullanılabilir. Ayrıca, modelin uygunluğunu değerlendirmek için hesaplanan R kare değeri veya regresyon katsayıları da kaydedilebilir. Bu değerlerin analiz sonuçlarına dayanarak yorumlanması ve daha fazla bilgi edinmek için ilgili kaynaklara başvurulması önemlidir.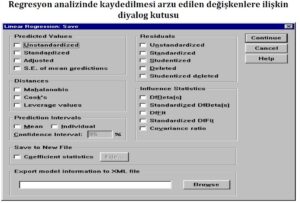
Kaynak: Altunişik, R., Coşkun, R., Bayraktaroğlu, S., & Yildirim, E. (2007). Sosyal bilimlerde araştırma yöntemleri. Sakarya Yayıncılık, Sakarya, 226, 103-118.
Bu örnekte, bir atletizm kampında yapılan regresyon analizi sonucunda, atletlerin koşma performansları ve kilo kayıpları incelenmektedir. İlk olarak, tek değişkenli regresyon analizi yapılarak, atletlerin koşma performansı ile diyet arasındaki ilişki değerlendirilmiştir. Tablo 1’de, koşma performansını tahmin etmek için kullanılan diyet değişkeni ile ilgili katsayılar, standart hatalar ve istatistiksel anlamlılık düzeyleri verilmektedir. Bu analiz sonucunda, diyet değişkeninin koşma performansı üzerinde anlamlı bir etkisinin olduğu görülmektedir.
Daha sonra, çok değişkenli regresyon analizi yapılarak, kilo kaybını belirleyen faktörlerin neler olduğu incelenmiştir. Tablo 2’de, kilo kaybını tahmin etmek için kullanılan değişkenler (diyet, eğitim süresi ve cinsiyet) ile ilgili katsayılar, standart hatalar ve istatistiksel anlamlılık düzeyleri sunulmaktadır. Bu analizde, diyet, eğitim süresi ve cinsiyet değişkenlerinin kilo kaybını etkileyen önemli faktörler olduğu görülmektedir.
Bu regresyon analizi sonuçlarına dayanarak, araştırmacı diyetin atletlerin koşma performansı üzerinde etkili olduğunu ve kilo kaybını belirleyen temel faktörlerin diyet, eğitim süresi ve cinsiyet olduğunu gözlemlemektedir. Ancak, analiz sonuçlarının daha detaylı bir şekilde değerlendirilmesi ve istatistiksel anlamlılığın yanı sıra pratik önemi de göz önünde bulundurulması önemlidir.
Kaynak: Altunişik, R., Coşkun, R., Bayraktaroğlu, S., & Yildirim, E. (2007). Sosyal bilimlerde araştırma yöntemleri. Sakarya Yayıncılık, Sakarya, 226, 103-118.
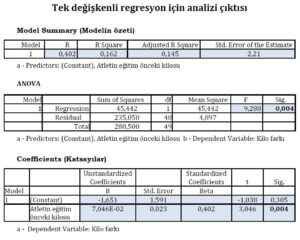
Yukarıdaki tablodan elde edilen tek değişkenli regresyon analizi sonuçlarına göre, regresyon modelinin anlamlı olduğunu söyleyebiliriz. Bunun sebebi, F (9.280) değerinin p<0.004 istatistiksel anlamlılık düzeyinden küçük olmasıdır. Bu sonuçlar, atletin eğitim öncesi kilosunun kilo farkını açıklamada önemli bir faktör olduğunu göstermektedir. R2 değeri 0.162 olduğundan, atletin eğitim öncesi kilosunun kilo farkındaki değişimin sadece %16.2’sini açıklayabildiğini gözlemlemekteyiz. Ayarlanmış R2 değeri ise 0.145 olduğundan, bu açıklama oranının %14.5’e düştüğünü göstermektedir. Modelde yer alan bağımsız değişkene ait katsayı 0.0706 (7,046 E02) olarak hesaplanmıştır ve buna karşılık gelen beta (standardize edilmiş regresyon katsayısı) değeri 0.402’dir. Bu beta değeri, atletin eğitim öncesi kilosunun kilo farkındaki değişime istatistiksel olarak anlamlı bir katkı sağladığını ifade etmektedir. Daha basit bir ifadeyle, eğitim öncesi kilosunda meydana gelecek bir standart sapmalık artış, kilo farkında 0.402 standart sapmalık bir kilo kaybı ile sonuçlanacaktır. Bu sonuçlar, atletlerin kilo kaybını etkileyen faktörlerin başında eğitim öncesi kilolarının geldiğini göstermektedir. Ancak, diğer değişkenlerin etkisini de değerlendirmek ve daha kapsamlı bir yorum yapmak için regresyon analizi sonuçlarını daha ayrıntılı bir şekilde incelemek önemlidir.
Verilerinizin analizi ve yorumlanması konusunda, akademik alanda her konuda yardıma ihtiyacınız varsa, uzman ekibimizle birlikte size yardımcı olmaktan mutluluk duyarız. Projelerinizin gereksinimlerini değerlendirebilir, size en uygun hizmetleri sunabiliriz. İletişime geçmek ve daha fazla bilgi almak için bize ulaşabilirsiniz.

